Computer Graphics
CSE 5280 Clipping

References

• Computer Graphics: Principles and Practice Second Edition in C, Foley, van Dam, Feiner and Hughes © 1998
• Procedural Elements for Computer Graphics, Rogers, David F. © 1985 by McGraw-Hill, Inc.
• On-line Computer Graphics Clipping tutorial

Clipping Volumes

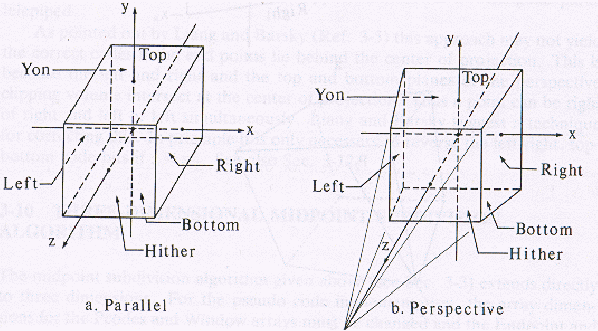
There are 2 common 3D clipping volumes

1. Rectangular parallelepiped (box) used for parallel or axonometric projections
2. The truncated pyramidal volume, sometimes called the frustum of vision, used for perspective projections. A frustum is basically a 3d pyramid, with the top lopped off.

Each of these volumes are six-side; see illustration below.

Clipping

The Cohen-Sutherland and Cyrus-Beck line-clipping algorithms can be extended for 3D. For 3D clipping, a 6-bit end point code is used. Bit#1 is the rightmost bit.

Cohen-Sutherland 3D Line Clipping

Canonical Parallel View Volume
Bit	Condition Test
bit#1	point is above the view volume ( y > 1 )
bit#2	point is below the view volume ( y < -1 )
bit#3	point is right of the view volume ( x > 1 )
bit#4	point is left of the view volume ( x < -1
bit#5	point is behind the view volume ( z < -1 )
bit#6	point is in front of the view volume ( z > 0 )

Canonical Perspective View Volume
Bit	Condition Test
bit#1	point is above the view volume ( y > -z )
bit#2	point is below the view volume ( y < z )
bit#3	point is right of the view volume ( x > -z )
bit#4	point is left of the view volume ( x < z )
bit#5	point is behind the view volume ( z < -1 )
bit#6	point is in front of the view volume ( z > z(min) )

Steps using the endpoint codes

1. If both endpoints have the code 000000, the the line is trivially accepted (visible).
2. If the logical AND (&) of the codes is not zero, then the line can be trivially rejected (not visible).
3. If the logical AND (&) of the codes is zero, then iterative clipping takes place.

Parametric 3D Line Clipping

Parametric 3D line representation

Line ===> P0(x0, y0, z0) to P1(x1, y1, z1)

1. x(t) = x0 + t(x1 - x0)
2. y(t) = y0 + t(y1 - y0), 0 <= t <= 1
3. z(t) = z0 + t(z1 - z0)

Note: t varies from 0 to 1

Calculate the intersection of a line with a plane

Let's consider the y = 1 plane ( Parallel )
2. --> 1 = y0 + t * (y1 - y0) or t = 1 - y0 / y1 - y0, if t is [0, 1] then substitute for t in equations below
1. --> x = x0 + 1 - y0 / y1 - y0 * (x1 - x0)
3. --> z = z0 + 1 - y0 / y1 - y0 * ( z1 - z0)

Let's consider the y = z plane ( Perspective )
2. & 3. --> y0 + t * (y1 - y0) = z0 + t * (z1 - z0) or t = z0 - y0 / (y1 - y0) - (z1 - z0)
1. --------> x = x0 + (x1 - x0) * ( z0 - y0) / (y1 - y0) - (z1 - z0)
2. --------> y = y0 + ( y1 - y0) * ( z0 - y0) / (y1 - y0) - (z1 - z0)
3. --------> z = y

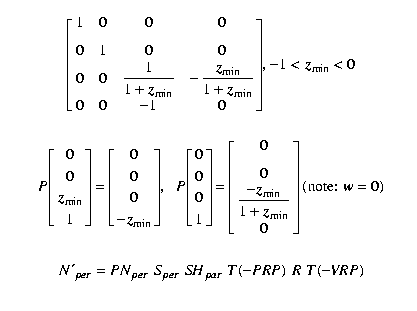
The reason for choosing this canonical view volume is to simplify the intersection computations.

Other Clipping Algorithms

Cyrus-Beck
Sutherland-Hodgeman
Liang-Barsky

Clipping in Homogeneous Coordinates

Why?

Simplification and efficiency - Transform the perspective-projection canonical view volume into the parallel-projection view volume and the sam clip procedure for both cases.
Clipping must be done in homogeneous coordinates to ensure correct results. This type of clipping is typically implemented in hardware.

Problems

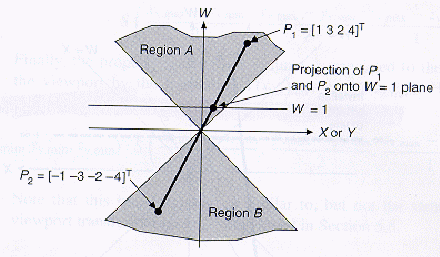
Homogenization can cause problems in 3D clipping if w < 0

Transformation from Perspective-projection to Parallel-projection canonical view volume

Defining the View Volume in homogeneous coordinates

Parallel Projection View Volume definition	Inequalities in homogeneous coordinates	Corresponding Plane equations
-1 <= x <= 1	-1 <= X/W <= 1	-W <= X <= W
-1 <= y <= 1	-1 <= Y/W <= 1	-W <= Y <= W
-1 <= z <= 0	-1 <= Z/W <= 0	-W <= Z <= 0

Constraints

• Case 1: W > 0: -W <= X <= W, -W <= Y <= W, -W <= Z <= 0
• Case 2: W < 0: -W >= X >= W, -W >= Y >= W, -W >= Z >= 0

Problema

Solutions:

Examples

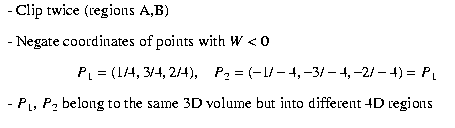
Cohen-Sutherland Clipping Example ---> Run Here , Source Code ---> Here