Computer Graphics
CSE 5280 Math Fundamentals

Math Fundamentals

References

• Matrix Math Basics
• Plane and Solid Analytic Geometry, Joseph H. Kindle
• WWW Math Tutorial

  Rectangular Coordinates

  Plane is divided into 4 quadrants by 2 perpendicular lines intersecting at the origin point O. The distance from the X axis is the y-coordinate (ordinate) the distance from the Y axis is the x-coordinate (abscissa).

  Distance between 2 points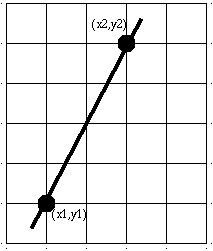

  The distance between two points P1(x1,y1) and P2(x2,y2) is found by using the Pythagorean Theorem:
  
  D = SQRT( (x2-x1)^2 + (y2-y1)^2)

  Midpoint of a Line

  The midpoint, M, of a line segment P1(x1,y1) to P2(x2,y2) is given by:
  
  MP = (x,y) = ((x1+x2/2), (y1+y2)/2)

  
  Slope of a line passing through 2 Points

  The slope of a line is defined as the tangent of the angle of inclination. Thus M = TAN(THETA) where THETA is the angle of inclination and M is the slope. The slope through 2 points is:
  
  M = TAN(ø) = (y2 - y1) / (x2 - x1)

  
  
  Test for Perpendicular and Parallel Lines

  Two lines with slopes M1 and M2 are perpendicular if:

  • M1 = -1/M2 or M1 * M2 = -1
  • the cosine of the angle between them is 0

  
  Two lines are parallel when their slopes M1 and M2 are equal.

  
  Parametric form of a Line

  Given points P1 = (x1,y1) and P2 = (x2,y2), the parametric form for a line is:
  
  x = x1 + t(x2-x1)
  y = y1 + t(y2-y1)
  0 <= t <= 1
  
  t is called the parameter. When t = 0 we get P1 and when t = 1 we get P2. As t varies between 0 and 1, we get all the other points on the line
  segment between P1 and P2.

  Polar Coordinates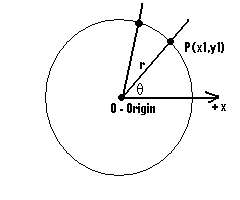

  A polar coordinate (in 2 dimensions) is an ordered pair (r, theta) which are defined as follows. For a point, P, r is the distance from the origin to P. Theta is the angle between the x-axis and the line segment from P to the origin. Notice that there is more than one valid value for theta. For example, if the angle between the x-axis and the line segment is 30 degrees, valid values of theta are (in degrees):
  30, (30+360) = 390, (390+360) = 750, etc.
  
  The use of polar (instead of Cartesian) coordinates can simplify some calculations.

  Changing Coordinate Systems

  Changing from Polar to cartesian coordinates :
  x = r × cos(ø), y = r × sin(ø)
  Conversely, changing from Cartesian coordiantes to Polar:
  r² = x²+ y², ø = arctan(y/x)

Vectors

A vector is a directed line segment, characterized by its length and direction.

Vector Properties

Vectors have special arithmetic properties:

1. If A is a vector, then -A is a vector with same length as A but pointing in the opposite direction.
2. If A is a vector, the kA is a vector whose direction is the same as or opposite that of A, depending on the sign of the number k, and whose length is k times the length of A. This is an example of scalar multiplication.
3. Two vectors can be added together to produce a third vector by using the parallelogram method or the head-to-tail method. This is an example of vector addition.

In the parallelogram method, vectors A and B are placed tail to tail. Their sum A + B is the vector determined by the diagonal of the parallelogram formed by the vectors A and B. In the head-to-tail method, the tail of B is placed at the head of A. The vector A + B is determined by the line segment pointing from the tail of A to the head of B. Both methods yield the same results, however the head-to-tail method is easier when adding multiple vectors together. See figure below.

The dot product

The dot product can be used to generate vectors whose length is 1, this is called normalizing a vector. To nomalize a vector v, we simply compute v´ = v / ||v||. The resulting vector has a length 1, and is called the unit vector.
Dot products can also be used to measure angles. The angle between the vectors v an w is

COS - ¹ ( v . w / ||v|| ||w|| )

Note that, if v and w are unit vectors, then the division is unnecessary. Dot product characteristics include the following:

• Vectors a and b are perpendicular if (a . b) = 0.
• Vectors a and b are < 90 degrees apart if (a . b) > 0;
• Vectors a and b are > 90 degress apart if (a . b) < 0;

Example:

Calculate the angle between the vectors a = 3i + 5j and b = 2i + j, shown the figure below:

		
			|| a || = (x1)² + (y1)²     || b || = (x2)² + (y2)²
				    = (3)² + (5)²              = (2)² + (1)²
				    = 9 + 25                   = 4 + 1
                  = SQRT(34)                 = SQRT(5)
             
             a . b = (x1 × x2) + (y1 × y2)
                   = (3 × 2) + (5 × 1)
                   = 6 + 5 = 11
                 ø = COS-¹ (11/( SQRT(34) × SQRT(5) ))
                 ø = COS-¹ (11/ SQRT(170)) 
                 ø = COS-¹ (11/13.038) = COS-¹(.84368) = 32.47