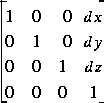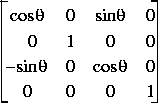Translate
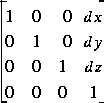
Rotate about X-Axis

Rotate about Y-Axis
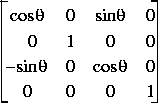
Rotate about Z-Axis

Example(s)
Like 2D transformations, 3D transformations can be represented using homogeneous coordinates by 4 × 4
matrices, providing we represent our points using homogeneous coordinates.
P = (x,y,z) ----> P´ = (x,y,z,W)
The corresponding point in 3D is P = (x/W, y/W, z/W)
Note: All transformations below apply to a right-handed coordinate system
Scaling changes the dimension of an object. The scale factor S determines whether the scaling is magnification, S > 1, or a reduction, S < 1. Scaling with respect to the origin, where the origin remains fixed is represented by the scale matrix below.