Transformation Supplement

Transformation Summary

2D Transformations

shear x matrix
  1.0, Shx, 0.0,
  0.0, 1.0, 0.0,
  0.0, 0.0, 1.0
 
shear y matrix
  1.0, 0.0, 0.0,
  Shy, 1.0, 0.0, 
  0.0, 0.0, 1.0
 
scaling matrix
  Sx,  0.0, 0.0,
  0.0, Sy,  0.0,
  0.0, 0.0, 1.0
  
Reflection about the y-axis
 -1.0, 0.0, 0.0, 
  0.0, 1.0, 0.0, 
  0.0, 0.0, 1.0
  
Reflection about the x-axis
  1.0, 0.0,  0.0, 
  0.0, -1.0, 0.0, 
  0.0, 0.0,  1.0
  
Reflection about the origin
  -1.0, 0.0,  0.0, 
  0.0,  -1.0, 0.0, 
  0.0,  0.0,  1.0
  
Reflection about the line y=x
  0.0, 1.0, 0.0, 
  1.0, 0.0, 0.0, 
  0.0, 0.0, 1.0
  
translation matrix
  1.0, 0.0, Tx,
  0.0, 1.0, Ty,
  0.0, 0.0, 1.0
  
rotation about origin 
 cos(radians),  -sin(radians), 0.0,
 sin(radians),   cos(radians), 0.0,
 0.0,            0.0,          1.0
  
rotation about an arbitrary point
  cos(radians),  -sin(radians), x * (1 - cos(radians)) + y * sin(radians),
  sin(radians),  cos(radians),  y * (1 - cos(radians)) + x * sin(radians),
  0.0,           0.0,           1.0
  
scaling about an arbitrary point
  Sx,  0.0, x * (1 - Sx),
  0.0, Sy,  y * (1 - Sy),
  0.0, 0.0, 1.0
  
invert matrix
  -1.0, 0.0,  0.0,
  0.0,  -1.0, 0.0,
  0.0,  0.0,  -1.0
  

3D Transformations





  
  

    
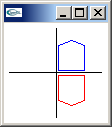
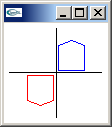
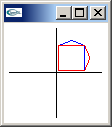
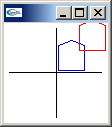
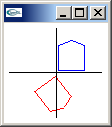
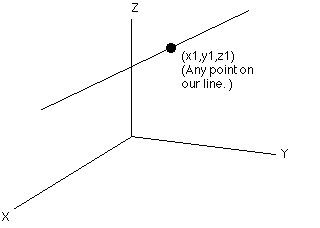
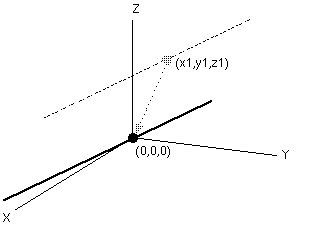
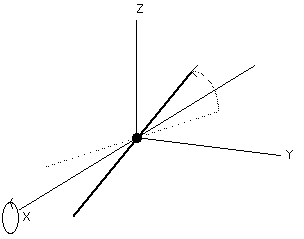
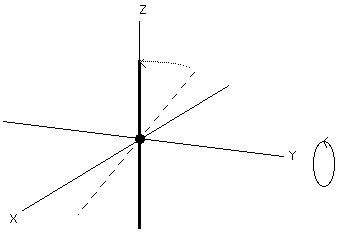
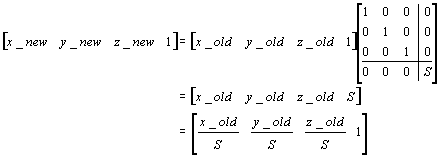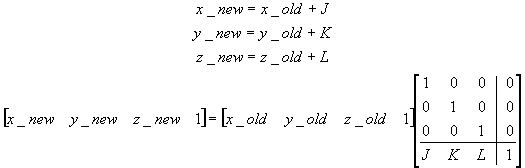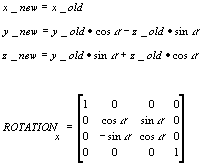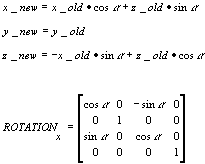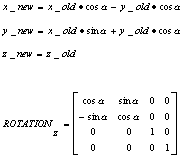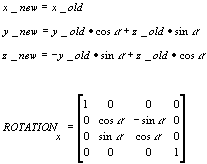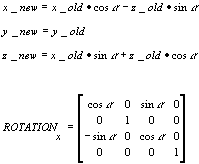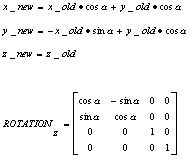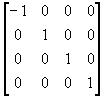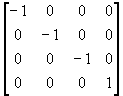invert matrix
 -1.0, 0.0,  0.0,  0.0,
  0.0, -1.0, 0.0,  0.0,
  0.0, 0.0,  -1.0, 0.0,
  0.0, 0.0,  0.0,  -1.0

    

  

    
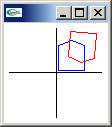
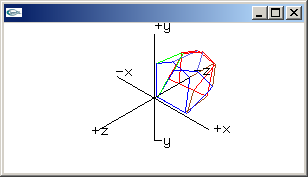
shear x matrix
  1.0, Shxy, Shxz, 0.0,
  0.0, 1.0,  0.0,  0.0,
  0.0, 0.0,  1.0,  0.0,
  0.0, 0.0,  0.0,  1.0

    

  

    
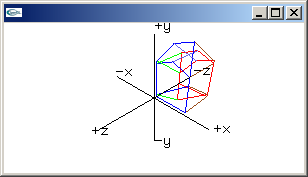
shear y matrix
  1.0,  0.0, 0.0,  0.0,
  Shyx, 1.0, Shyz, 0.0,
  0.0,  0.0, 1.0,  0.0,
  0.0,  0.0, 0.0,  1.0

     

  

    
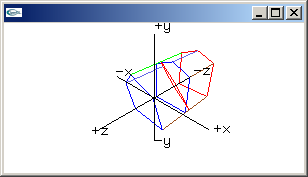
shear z matrix
  1.0,   0.0, 0.0, 0.0,
  0.0,   1.0, 0.0, 0.0,
  Shzx, Shzy, 1.0, 0.0,
  0.0,   0.0, 0.0, 1.0

     

  

    
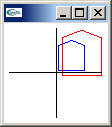
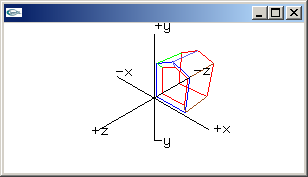
shear xy matrix
  1.0,  0.0, Shxz, 0.0,
  0.0,  1.0, Shyz, 0.0,
  0.0,  0.0, 1.0,  0.0,
  0.0,  0.0, 0.0,  1.0

     

  

    
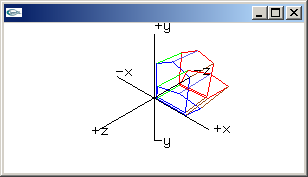
shear xz matrix
  1.0,  Shxy, 0.0, 0.0,
  0.0,  1.0,  0.0, 0.0,
  0.0,  Shzy, 1.0, 0.0,
  0.0,  0.0,  0.0, 1.0

     

  

    
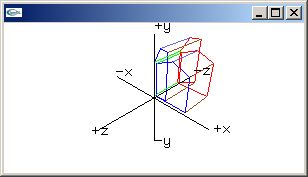
shear yz matrix
  1.0,   0.0, 0.0, 0.0,
  Shyx,  1.0, 0.0, 0.0,
  Shzx,  0.0, 1.0, 0.0,
  0.0,   0.0, 0.0, 1.0

     

  

    
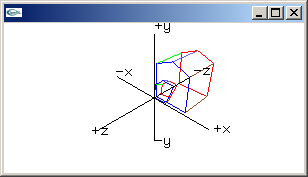
shear xyz matrix
  1.0,   Shxy, Shxz, 0.0,
  Shyx,  1.0,  Shyz, 0.0,
  Shzx,  Shzy, 1.0,  0.0,
  0.0,   0.0,  0.0,  1.0

     

  

    
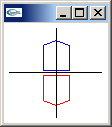
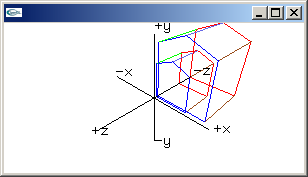
scaling matrix
  Sx,  0.0, 0.0, 0.0,
  0.0, Sy,  0.0, 0.0,
  0.0, 0.0, Sz,  0.0,
  0.0, 0.0, 0.0, 1.0

    

  

    
translation matrix
  1.0, 0.0, 0.0, Tx,
  0.0, 1.0, 0.0, Ty,
  0.0, 0.0, 1.0, Tz, 
  0.0, 0.0, 0.0, 1.0

    

  

    
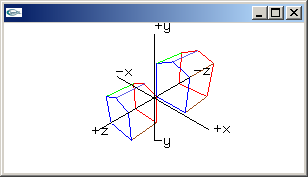rotation x-axis matrix
  1.0, 0.0,          0.0,           0.0, 
  0.0, cos(radians), -sin(radians), 0.0,
  0.0, sin(radians), cos(radians),  0.0,
  0.0, 0.0,          0.0,           1.0

    

  

    
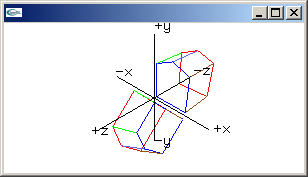rotation y-axis matrix
  cos(radians),  0.0, sin(radians), 0.0,
  0.0,           1.0, 0.0,          0.0, 
  -sin(radians), 0.0, cos(radians), 0.0,
  0.0,           0.0, 0.0,          1.0

    

  

    
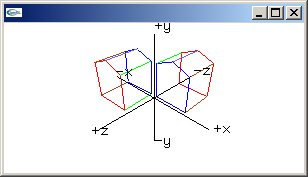rotation z-axis matrix
  cos(radians), -sin(radians), 0.0, 0.0,
  sin(radians), cos(radians),  0.0, 0.0,
  0.0,           0.0,          1.0, 0.0, 
  0.0,           0.0,          0.0, 1.0

    

  

    
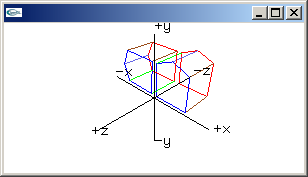Rotate [ x y z ] about the unit vector [ x y z ]T by radians

  s = sin(radians);
  c = cos(radians);
  c_1 = 1 - c;
  x*x*c_1+c,    x*y*c_1-z*s, x*z*c_1+y*s, 0.0,
  x*y*c_1+z*s,  y*y*c_1+c,   y*z*c_1-x*s, 0.0,
  x*z*c_1-y*s,  y*z*c_1+x*s, z*z*c_1+c,   0.0, 
  0.0,          0.0,         0.0,         1.0


     

  

    
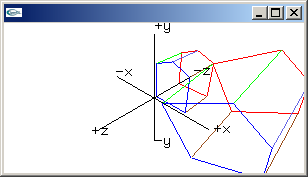Reflection through y-z plane: x -> -x, y -> y, z -> z  
 -1.0, 0.0, 0.0, 0.0,
  0.0, 1.0, 0.0, 0.0,
  0.0, 0.0, 1.0, 0.0,
  0.0, 0.0, 0.0, 1.0

    

  

    
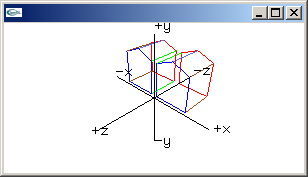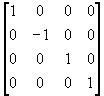
Reflection through x-z plane: x -> x, y -> -y, z -> z  
  1.0, 0.0,  0.0, 0.0,
  0.0, -1.0, 0.0, 0.0,
  0.0, 0.0,  1.0, 0.0,
  0.0, 0.0,  0.0, 1.0

    

  

    
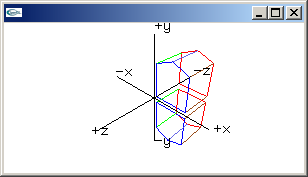Reflection through x-y plane: x -> x, y -> y, z -> -z  
(Convert RH coordinates to LH coordinates)
  1.0, 0.0, 0.0,  0.0,
  0.0, 1.0, 0.0,  0.0,
  0.0, 0.0, -1.0, 0.0,
  0.0, 0.0, 0.0,  1.0

    

  

    
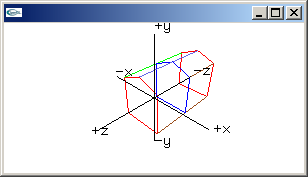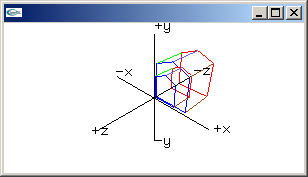
inverse scaling matrix
  1/Sx, 0.0,  0.0,  0.0,
  0.0,  1/Sy, 0.0,  0.0,
  0.0,  0.0,  1/Sz, 0.0,
  0.0,  0.0,  0.0,  1.0

     

  

    
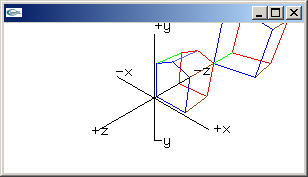
inverse translation matrix
  1.0, 0.0, 0.0, -Tx,
  0.0, 1.0, 0.0, -Ty,
  0.0, 0.0, 1.0, -Tz, 
  0.0, 0.0, 0.0, 1.0

     

  

    
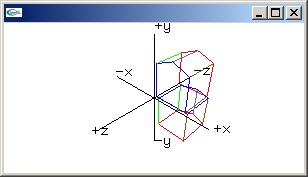
inverse rotation x-axis matrix
  1.0, 0.0,           0.0,          0.0, 
  0.0, cos(radians),  sin(radians), 0.0,
  0.0, -sin(radians), cos(radians), 0.0,
  0.0, 0.0,           0.0,          1.0

     

  

    
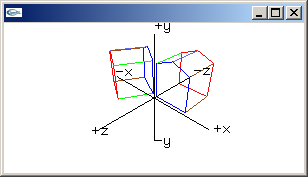
inverse rotation y-axis matrix
  cos(radians), 0.0, -sin(radians), 0.0,
  0.0,          1.0, 0.0,           0.0, 
  sin(radians), 0.0, cos(radians),  0.0,
  0.0,          0.0, 0.0,           1.0

     

  

    
rotation z-axis matrix
  cos(radians),  sin(radians), 0.0, 0.0,
  -sin(radians), cos(radians), 0.0, 0.0,
  0.0,           0.0,          1.0, 0.0, 
  0.0,           0.0,          0.0, 1.0

     

  

    
Scaling about a fixed point (XF, YF, ZF) can be carried out by
1. translating fixed point back to the origin.
2. scaling with the scaling matrix.
3. translating fixed point back to original position.
The overall matrix to achieve this is :
  Sx,        0.0,       0.0,      0.0,
  0.0,       Sy,        0.0,      0.0,
  0.0,       0.0,       Sz,       0.0,
  (1-Sx)*XF, (1-Sy)*YF, (1-Sz)*ZF 1.0

     






Rotation About an Arbitrary Axis :





In this case our rotational axis can be any straight line in 3D space.




There are 7 steps involved....


1.Translate to bring (x1, y1, z1) to origin.




2. Rotate about the x-axis until in xz plane.




3. Rotate about the y-axis.




Now our arbitrary line IS the z-axis so we


4. Rotate about the z-axis.




The final 3 steps are :


    
  
  1. Inverse of step 3. 
  
  2. Inverse of step 2. 
  
  3. Inverse of step 1. 


The complete procedure is represented by the formula,



  
Tr(-x1,-y1,-z1) . Rx(phi) . Ry(alpha) . Rz(theta) . Ry(-alpha) . Rx(-phi) 
  . Tr(x1,y1,z1) 
  
How do we calculate phi and alpha ?

  
Take an additional point on the line (x2, y2, z2);

  

  

  
cos(phi) = (z2 - z1)/d

  
sin(phi) = (y2 - y1)/d

  

  

  
cos(alpha) = d/e

  
sin(alpha) = (x2-x1)/e






Transformations in three-dimensions using homogeneous coordinates 


The usage of homogeneous coordinates in three-dimensional space 
makes it possible to represent all transformations in three-dimensional space by 
4x4 matrices:






The matrix can be partitioned as follows:




Scaling 

The following transformation performs local 
scaling:




Global scaling is performed by the following matrix:




Important: 


  
If the value of S is larger than one, then the size of the object is 
  reduced. 
If the value of S is less than one, then the size of the object 
  is increased. 
If global scaling is used, the fourth element of the vector 
  containing the result of this operation may not be equal to 1. Therefore this 
  vector has to be normalized. Then the new x, y and z homogenous coordinates 
  become cartesian ones.



Translation 

The following matrix translates a point 
(x_old, y_old, z_old) to a new point (x_new, y_new, z_new):




The relative movement of the point in x, y, z directories is presented by J, 
K and L. 

Rotation - Counterclockwise (positive):





  
  

    x axis rotation


    y axis rotation


    z axis rotation




Rotation - Counterwise (negative):





  
  

    x axis rotation


    y axis rotation


    z axis rotation



Rotation about arbitrary axes 

Rotations about arbitrary axes 
can be made up by several rotations about the x, y and z axes and by 
translations. The following sequence of steps provides a
universal proceeding 
for rotations about any arbitrary axis: 

1.Translate the arbitrary axis 
so that one of its endpoints coincides with the origin. 
2.Perform rotations 
about the x and y axes to align the arbitrary axis with the positive z axis. 

3.Rotate about the z axis by desired angle q.Apply the reverse rotations 
about the y and x axes. This will bring the arbitrary axis back to its original 
position from
the origin. 
4.Apply the reverse translation to place the 
arbitrary axis back in its initial position in place. 

All these 
transformations can be concatenated into a single matrix:




Reflection





  
  

    
      
Plane 

    
      
X=0 

    
      
Y=0 

    
      
Z=0 

    
      
Point (0,0,0) 

  

    
      
 

    
      
 

    
      
 

    
      
 

    
      
 






*This page suggested by J. Starkey. Some material from here