Computer Graphics
CSE 5280 Viewing Math Fundamentals

References

• Computer Graphics: Principles and Practice, Foley, van Dam, Feiner and Hughes, Addison-Wesley Inc, © 1997
• Dr. Shoaff's Perspective Projection Lecture
• On-line Introduction to View Transformation

The Viewing Pipeline



Characteristics of Projective Space

• Each point (x, y, z) in 3D space is represented by (wx, wy,wz, w), where w != 0
• Point (2, 3, 6, 2) , (4, 6, 12, 4), and (1, 2/3, 3, 1) all represent the same point in 3D projective space
• The "normalized" homogeneous points (x, y, z, 1) is often used
• A projective point with (x, y, z, 0) is considered to be at infinity
• Points at infinity represent a direction vector instead of a point
• Note: A problem with a perspective transformation is that it does not preserve straight lines or planes, i.e., straight lines are not transformed into straight lines and planes are no longer planar after the transformation.

Parallel Projections

Parallel View Volume

Perspective Projections

Perspective Projection View Volume

Compute 2D Coordinates from 3D Coordinates

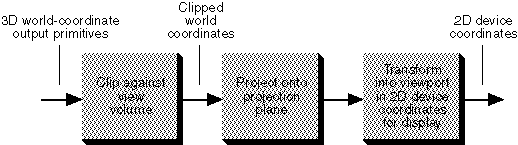
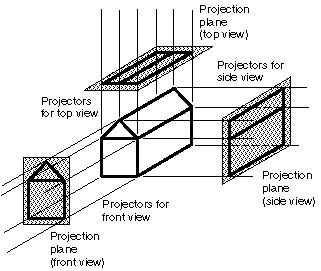
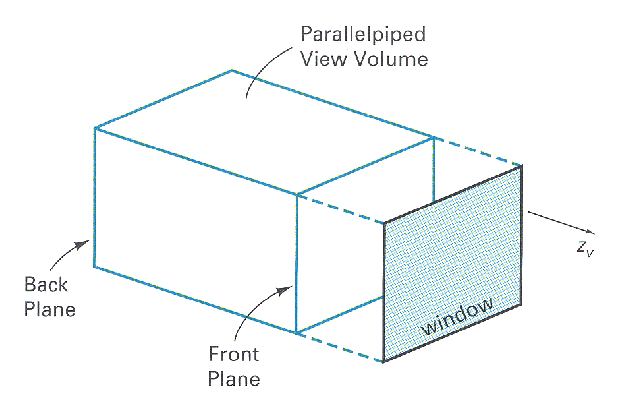
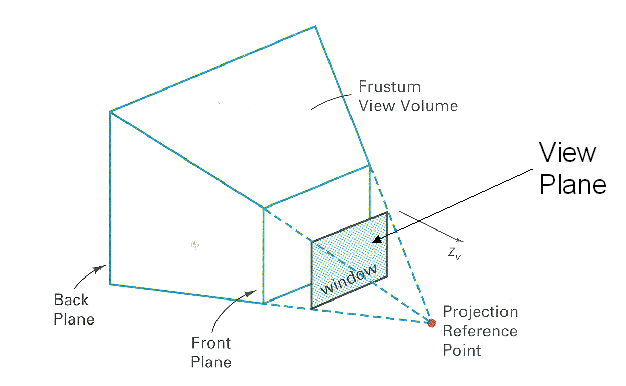
To simplify the math required for perspective projections, by placing the camera or eye in an axis-aligned configuration. Put the focal point at the origin and the view (projection) plane parallel to the XY-Plane at a distance D (focal length) from the origin.

To determine the projection of (x, y, z) onto the view (projection) plane at z = D, we use similar triangles to define the following ratios
xp / D = x / z; yp / D = y / z
xp / D * D = x / z * D ==> xp = x * D / z ,
yp / D * D = y / z * D ==> yp = y * D/z

Note how point (x, y, z) is projected to the view plane, to point ( xD/z, yD/z, D ). In this picture we are looking down the x-axis. We get something similar if we were looking down the y-axis. All values of z are allowed with the exception of z = 0. Points may be behind the center of projection as illustrated below.

Note that we can increase the perspective effect by decreasing D (moving closer). We can represent this in matrix form by using homogeneuos coordinates as follows:

[xh yh zh w] = [x y z 1] | 1 0 0 0 |
|0 1 0 0 |
|0 0 0 1/d |
|0 0 0 1 |

Example

Look at example of a 3D line in object space from:
P1 (x1 = 2.0, y1 = 5.0, z1 = 6.0) to P2 (x2 = 8.0, y2 = 7.0, z2 = 12.0)

In parametric form this line is represented as:
x(t) = 2 + 6 × t ==> x(t) = x1 + t(x2 - x1)
y(t) = 5 + 2 × t ==> y(t) = y1 + t(y2 - y1)
z(t) = 6 + 6 × t ==> z(t) = z1 + t(z2 - z1)

Let us choose an arbitrary value of t (t = 0.4) and compute the x, y, z values)

x = 2 + 6 × 0.4 = 4.4
y = 5 + 2 × 0.4 = 5.8 so Pi(t = 0.4) = (4.4, 5.8, 8.4)
z = 6 + 6 × 0.4 = 8.4

Now perform the perspective transformation (assume d = 10.0) for P1, Pi, P2. Then we get for the transformed points:

P1(x = 1.25, y = 3.125, z = 6); Pi(x = 2.39, y = 3.15, z = 8.4);
P2(x = 3.64, y = 3.18, z = 12)

If this is still a straight line then all three coordinates of point Pi must have the same value of the parameter t.

so for x we get 2.39 = 1.25 + t × (2.39) =>t = 0.48
for y we get 3.15 = 3.12 + t × (0.57) => t = 0.48
for z we get t = 0.40 since unchanged => therefore the points are not collinear.

To maintain linearity we can do a perspective depth transformation:

Zp = Z / (D + Z)

Then for point 1 Zp = 6 / (10+6) = .375
point 2 Zp = 12 / (10+12) = .545
point i Zp = 8.4 / (10+8.4) = .457

Now check with t value for point i 0.457 = 0.375 + t * (0.170) = .48. This is the same t value we got for point i x and y. Therefore points 1, 2, and i are still colinear after the perspective depth transformation.. Note that the relative z depth values remain unchanged, i.e. if Z1 < Z2 then Z1 / (Z1+d) < Z2 / (Z2+d) as shown below:

Z1 < Z2
Z1 × d < Z2 × d multiply both sides by d
(Z1 × Z2 + Z1 × d) < (Z1 × Z2 + Z2 × d) add Z1 × Z2 to both sides
Z1 × (Z2 + d) < Z2 × (Z1 + d)
Z1 / (Z1 + d) < Z2 / (Z2 + d)

Note that for Zp = Z / (Z+d) => 0 if d >> Z and => 1.0 if Z >> d
therefore 0.0 <= Zp <= 1.0

So to maintain linearity (or planarity) we must transform Z as well as X and Y.